
The picture above, for those who doesn't know, is a Klein bottle. It is the version of the Mobius strip in one more dimension. The surface has just one side and is non-orientable. This comes from a very interesting site I found one day when I was looking for something completely different in the Internet. Usually this is the way I find the most interesting sites. The site is:
Grand Illusions
It has 4 sections:
1. Toy Shop: in this section they sell a lot of interesting toys. Most, let's say, scientifically inclined. They are a little expensive, but they seem to be very well crafted. They have movies so you can see the toys in action. The Klein bottle of the picture can be purchased there.
2. Toy Collection: more interesting toys and objects, but they are not for sellling.
3. Optical Illusions: a collection of videos and pictures together with explanations. The interesting thing here is that they do not only restrict theirselves to the illusions already known by everyone, there are some modern ones as well.
4. Articles: brief articles about interesting stuff related to the other four sections.
I guess that it is worth to browse the website. I found it quite delighful.
Well, I'm a little pissed off today because me and my wife discovered that, although I am one year out of Brazil, we will have to pay the income tax there as well as here. Yes, we can deduct what we paid here, but here I am also paying the National Health System and a pension scheme, which I cannot deduce. Not a good week...
Well, let us come back to the science world. I was browsing the emails sent by one of my friends as he always send me interesting things and stumbled with the picture above and this link:
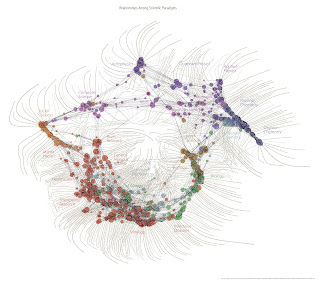
Scientific Method: Relationships Among Scientific Paradigms
It is a map relating branches of science whose credits go to Kevin Boyack, Dick Klavans and W. Bradford Paley. The idea is that each area of science, which they call a 'paradigm' and is represented by a circle, shares a link with another area if there is a scientific paper citing both together. I was examining the picture. It is a very beautiful one! But I noted an absence of direct links between the biology branches and physics. I guess that if you read some of my old posts, you know that in Statistical Physics there is a lot of papers relating such areas. For example, I would consider that at least some papers about Neural Networks can be considered related to Brain Research. There are also a lot of papers about the spread of diseases or the working of the immune system in Statistical Physics, which would add some direct links from the bottom to the top of the picture. In a not-so-humble move, I emailed one of the authors today talking about that and suggesting to add a separate circle for Statistical Physics. Come on, I agree it is a biased opinion, but I think that Statistical Physics deserves it.
I also find this page of the project Places & Spaces: Mapping Science, which is an exhibition of similar maps of all kinds of science studies which is touring the world. There are very nice and interesting pictures there and, for those who live here in UK like me, they may come to London and Oxford although the dates are not confirmed.
-------------------
I'm very pleased that Kevin Boyack answered my email so quickly. He explains the question I raised about Statistical Physics and his explanation helps in the understanding of the map:
1. The map is constructed by the most co-cited references, not the most recent ones. Therefore, it is natural that some more recent kinds of work are not present. Just the most refered to.
2. If Statistical Physics appears in these papers in a very interdisciplinary way, it would be spread out in the map and would not be easy to localize. But, as I said, if SP papers are not so cited as others, they will appear less.
3. The algorithm used to constructed the map only draws the strongest links to avoid a very crowded and difficult-to-see map. It is not that the links don't exist, they're just not so stronge as the other ones depicted.
Makes perfect sense. I would like to thank the author for such a nice and quick answer. This is really a very beautiful work.

After three weeks fighting against an horde of evil bacteria which were trying to eat me alive, I finally have some time to write. It looks a little exaggerated, but apart from the word 'evil' and the fact that it may well be a virus, the rest is true.
Okay, back to physics. While I was in home these days I was studying a little of Loop Quantum Gravity. LQG is also called Canonical Quantum Gravity because the idea is to try to quantize gravity without using perturbative methods by a technique called canonical quantization. Now, instead of talking about what is canonical quantization, I would like to go through another path. I would like to talk about the more general procedure named 'quantization'. I decided to write about it because in one of the papers I was reading the author wrote that LQG was based in a well understood quantization procedure. I do not deny that canonical quantization is a well understood method to transform a classical theory in a quantum one mathematically, but this rang a bell in my head because, in the end, the whole thing of 'quantizing' is, in reality, far from being well understood conceptually. Let me explain better.
Quantum Mechanics is believed to be the true fundamental theory of nature. There is little doubt about that given the overwhelming experimental evidence in favor of it. So, the aim is to make all known theories compatible with QM. But nobody really knows what is the real principles of QM. Yes, this is the truth. However, using a lot of analogies, genial insights and mathematical efforts, we were able to make 3 of the 4 forces known in nature compatible with what we know is true in QM. Nowadays, after more than a century of QM, it seems that we are on our way to quantize the last one, namely gravity, using again mathematical analogies. These mathematical analogies are called quantization methods, but they are exactly that: mathematical techniques. We substitute real variables by hermitian operators, real Poisson brackets by commutators, expand the solution of the equations in Fourier series and define creation and annihilation operators but, what is really going on here, nobody truly knows.
The problem is that is quite embarassing for a theory that should be the fundamental one when we have to derive its equations first from the not-so-correct one and then quantizing (modifying following some recipe) it. Conceptually, it would be desirable to start with some quantum mechanical principles, derive the QM equations and, through some limit, recover the classical results. This would be the ideal, but it seems that we are far away from this goal. And maybe that is the reason why gravity is so difficult to quantize and why there are those incovenient infinities in quantum field theory. Probably, when we find the true quantum principles, we will discover that all the quantization methods are thumb rules to go from one limit to another. This is a difficult endeavour and maybe the solution would just appear when we discover new phenomena or maybe when someone have a strikingly new idea. I will risk to say that this would be still even more exciting than even quantizing gravity, for it would change (again) completely our view of nature.
I'll be optimist and hope that I can see it still in my lifetime. There are quite a lot of clever people working on these matters today. There are the Bayesian approaches, the more or less old Bohmian Mechanics, Nelson's QM and a lot of other tentatives, but something is still lacking. I believe that when the answer comes it will be like when you learn relativity: "Why did nobody think about it before? It's so obvious!" I mean, it is that feeling that every piece has fitted together. Well, I'll wait. :)
Picture: Taken from the University of Tokyo's Website.


